2. The Solution: PrivateNess Network
Litepaper
GRC’s Ultra–High Entropy PRNG with PrivateNess dual fast-finality deterministic cryptocurrencies meet Emercoin to abstract, obfuscate and over-deliver on the task at hand. We use the carefully designed Ultra-High Entropy PRNG based on Latin Squares that utilizes more than 1536 bits of internal “state” memory made FOSS by Gibson Research Corporation. Easily overlooked are the intrinsic benefits of Randpay’s Blum’s “coin-flipping-by-telephone” problem resolution provided. Zero-Trust in the purest sense of the term where Trust is well-placed: start and stop at one self from the consumer perspective. “Trust no One, Trust Anyone” meaning has evolved since Turing-completeness, with regards and respect to ARPA Chain (Blog: ‘ARPA Threshold BLS Random Number Generator Design’).
2.1 A fully Decentralized and Obfuscated OSI protocol stack
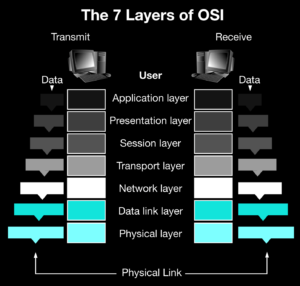
PrivateNess Network’s NESS token is a dual coin Fiber chain cryptocurrency on the Skycoin platform and equipped with Emercoin core (EmerNVS) as a local BaaS provider through json-rpc endpoints. The two technologies will be working side-by-side in a SHA-256 signed public-key to public-key communication scheme, unaware of one another in a kind of Double-Blind operation. Communications are limited to json-rpc respective endpoints restricted to 127.0.0.1 hence dramatically reducing surface and attack vectors. To the best of our current knowledge, this architecture has no functional limitations of any kind, no single point of failure and presents the emergence of decentralized oracle capability from the dual ledger design as well as native support for non-fungible digital assets.
– NESS Network: Low-power hardware hence sustainable
– EmerNVS: General purpose Name-Value System to store data and digital assets
– Skywire: End-to-end (e2e) encrypted mesh VPN
Backed by such natives features, NESS doesn’t rely on any centralized protocols and short of shutting down the entire Internet we would be at loss to find anyone or anything that could interfere with it.
2.2 Uniqueness & Determinacy
Repeatedly generating and selecting a biased random number is not expected for the security-sensitive applications that rely on randomness. Uniqueness is a stricter requirement than determinacy. Determinacy only requires that the random generation procedure involves no randomness.
2.3 Non-interactiveness
On the blockchain, it is natural to generate random numbers in a decentralized way. However, the communication overhead will become a limitation or a single point of failure of the whole system. ‘ Elliptic Curve Digital Signature Algorithm (ECDSA) can be redefined to satisfy determinacy but not uniqueness and communication overhead can lead to single-point-of-failure of the whole system.
Group size
Tolerable node failure
System failure
51
24.2%
0.0105%
101
31.1%
0.0104%
201
36.7%
0.0106%
501
41.6%
0.0108%
Source: https://arpa.medium.com/arpa-threshold-bls-random-number-generator-design-2b7a6e7f7826
With PrivateNess decentralized PKI and operations the group size is utility rather than metric; it can scale up or down indifferently, node failure can be All but 1 block publisher theoretically, the chain will run in read only mode even if block-publisher goes offline and even then it wouldn’t affect existing services, System failure are mitigated between 2 blockchains running battle-tested tech (Emercoin, Genesis 2013 and Skycoin, Genesis 2014).
2.4 We don’t put all our Trust in the same basket
Emercoin URIs are BIP21 and due to it’s extremely light footprint, Emercoin daemons are running on all incentivized PrivateNess nodes. That’s how we are resistant to Phantom nodes like the PIVX and all masternode systems that can run Golang forks. In smart contract environments, randomness sources that satisfy the uniqueness, determinacy and non-interactiveness imply relatively complex aggregation mechanisms and consensus to protect the consumer’s trust in the system.
With PrivateNess we turn tables on Trust versus System versus Decentralization. Who should trust what, and why should anyone trust anything when not necessary? We empower the consumer as much or as little as desired, depending on the privateness and ownership of the seedkey used to initialize the non-repeating 1536 bits entropy PRNG. The consumer can be a human, a smart contract or both in such a way that any cryptographic system will recognize (or not if malicious).
Acquire or Register a Non-Fungible PrivateNess asset for randomness depending on uniqueness of seedkey used at PRNG initialization.
Subscribe to Randomness with the ID obtained earlier: Initialize PRNG with seedkey;
Initiate a Randpay tx with 1/1 Risk to pay with short timeout to force an onchain event; for when 3rd party need to verify origin and unbiasedness
Note: This Private and Public seedkey approach make for a simpler and lighter implementation of BLS signatures for consensus verifiable by 3rd parties; and outsourced to a foreign blockchain secured by Bitcoin hash power through merged-mining PoW.
2.5 More about UHE-PRNG
It uses a “safe prime” factor to guarantee that every possible PRNG “state” is visited before the sequence begins to repeat. The result is that the “period” of this generator will be the “Germain prime” 1,768,863 x 2E1535 – 1, which is approximately 2.132 x 10E468. This is such a large number that it might as well be infinite.
You find our Ultra High Entropy Pseudo Random Number Generator on GitHub: https://github.com/NESS-Network/PyUHEPRNG
2.6 This generator effectively never repeats
For our purposes, a “SeedKey” is used to initialize the PRNG to a pseudo-randomly chosen point in this incredibly large loop of unpredictable pseudo-random numbers, from which we then pull as many pseudo-random values as we need. The 256-character “SeedKey” uses the 94 printable ASCII characters (spaces are ignored). Therefore, this yields 94E256 possible seedkeys. This is 1.32 x 10E505 possible strings, which is equivalent to 1,678 bits of entropy. Since this is greater than the total entropic state of the UHEPRNG, a SeedKey of this length and complexity is sufficient (and necessary) to fully initialize a PRNG of this complexity.
Not only is it an extremely good pseudo-random number generator, it is also extremely fast.
This makes its use with slow processors, or under interpreted languages (such as its implementation language, JavaScript) much more practical than many other much weaker PRNGs. Although mathematicians have been unable to determine how many different 26×26 Squares can be created, they have been able to determine that the number is at least 9.337 x 10E426, or approximately 2E1418. This is an incredibly large number. But for our purposes it is only meaningful if any of those many possible Latin Squares could potentially be generated by our OTG grid generator. If we were to use any traditional PRNG, even something state-of-the-art such as Fortuna, based upon a cryptographic symmetric cipher or a hash, we would be limited to generating Latin Squares from such a generator’s much lower level of entropy . . . on the order of 256 or 384 bits. This would be more than sufficient for many cryptographic applications, but not for ours. Since 26×26 Latin Squares are known to have a potential entropy of at least 1418 bits, we needed a PRNG that could keep up. So an “ultra-high entropy” PRNG, having an entropy of 1536 bits, was developed to allow access to all possible Latin Squares.
Not only do we want a system that is able to select one OTG grid from among the truly incredible number of possible Latin Squares, but every user needs to be able to regenerate their own personal one out of 10E427 grids if their existing paper copy should ever need to be replaced, resized, recolored, re-fonted, or reprinted for any reason. We achieve those two goals by generating and capturing a very long 1536-bit pseudo-random number — the “SeedKey” — then using that number to set the ultra-high entropy pseudo-random number generator’s 1536-bit “initial state” from which a single unique grid will be created.
2.7 More on Randpay
Transactions on Emercoin blockchain are non-monetary for the most part so far and near-free. This article describes a system for aggregating payments based on a zero-trust lottery protocol. We demonstrate its applicability to very large-scale settlements amounting to trillions of transactions per year. Under the protocol, the payment recipient creates a unique payment address and defines a space of possible payment addresses including this one.
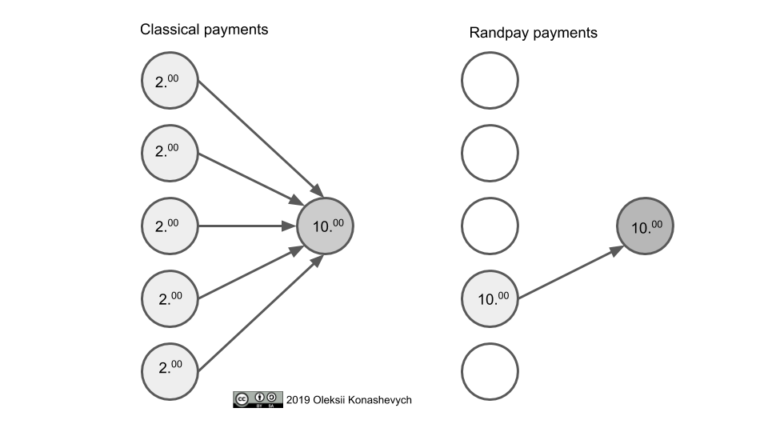
The payer chooses a random address from the specified space, creates a payment transaction to the selected address, and then sends the transaction to the payment recipient.
If the address specified in the received transaction matches the previously created one, the recipient signs the transaction and publishes it to the blockchain, and payment is transferred. If the addresses do not match, the transaction is deemed invalid and is ignored; only 1 in $risk trigger payment; or on demand with a 1 on 1.
In a typical Randpay scenario, the payment is unlikely in each particular “lottery” instance. But as the number of such instances is high, the balances of all participants will be updated in a fair way. This article presents a mathematical model proving that, for all the participants, Randpay will statistically converge to the fair amounts they would have received or sent without using this subsystem. In addition, Randpay reduces payers’ transaction costs, making it economically viable, especially for micro payments.
Last updated